University of Regina Math Trail
Created by EMTH 351
February 28, 2001
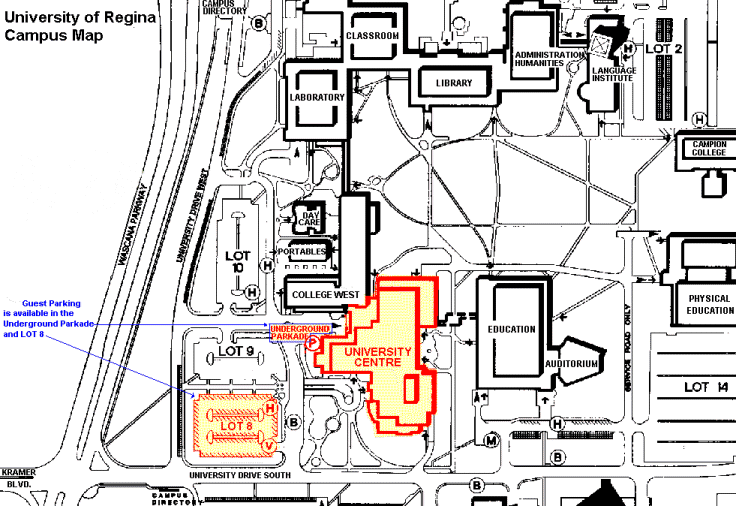
University of Regina - Campus Map
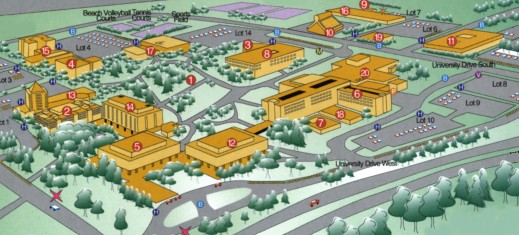
1. Academic Green |
11. ISM Building |
2. Administrative-Humanities Building |
12. Lab Building |
3. Education Auditorium |
13. Language Institute |
4. Campion College |
14. Dr. John Archer Library |
5. Classroom Building |
15. Luther College |
6. College West |
16. Maintenance Building |
7. Day Care |
17. Physical Education Building |
8. Education Building |
18. Portable Classrooms |
9. Engineering Garage |
19. Software Technology Centre |
10. Heating Plant |
20. Dr. Riddell Centre (University Centre) |
 Riddell Centre (Student Centre)
Riddell Centre (Student Centre)
As you enter the University Centre building you will notice a small convenience store called Golden Prairie Confections. Go inside and find out
the total cost for a bottle of V-8 Splash. What are the possible coin
combinations you could use to pay for this if you don't want any change
back?Now imagine you are a U of R resident student living in College West. You have just moved in and you haven't bought groceries yet. Suppose you have a
$50 budget for food for one 5-day school week and you must eat only at the U
of R University Centre food court and restaurants (except the Lazy Owl).
Write out your weekly budget of what and where you would eat.Take a look at the floor. Lots of squares, eh? Block off a 4 x 4 group
of squares. How many squares are there in this block? [Hint: not all
squares are the same size!]. Could you see a pattern in the way to count
them? Try a 3 x 3 block. Now try to predict how many squares there are in
an 8 x 8 block.Proceed to the indoor parking lot in the basement via the elevator. Have
a look at a Saskatchewan license plate. Note the 3-letter, 3-number form of
the standard (non-personalized) plates. How many different license plates
is it possible to make of this form? How many if you eliminate one letter?
How many if you eliminate one number?Have a look at the vehicles parked in the underground parking. How many
different ways can you think of to describe and represent the "population"
of vehicles parked in here? Pick one and draw the representation of it
below.Based on the vehicle population you found and assuming that each vehicle
is equally likely to be the next to leave, what is the probability that the
next vehicle to leave will be:
(a) blue?
(b) a truck?
(c) a Ford?
(d) a blue truck?
(e) a blue Ford?
(f) a Ford truck?
(g) a blue Ford truck?
College West 
Go to the mailboxes located by the resident office. Consider the shape of these mailboxes. What if they were circular, triangular or square? Why do you think they chose a rectangular shape?
Go to the mathematics section at the back of the bookstore. Find 10 different mathematics and statistics textbooks. Measure the volume of these textbooks (height of spine
 width of cover
width of cover  length of cover) and record their price. On the graph paper provided create a graph of price vs. volume.
length of cover) and record their price. On the graph paper provided create a graph of price vs. volume.Go to the Parking and Security Office. How much is a night parking pass? If you needed to attend a night class for two months (once a week for three hours over eight weeks) is it a better value to buy a parking pass or to park at a meter?
Lab Building

Find the map of the first floor of the lab building. Notice that there is not a scale on this map. Devise a scale for this map. How could you check to see if your scale is accurate? Is your scale accurate?
Across from the Lab Café there are orange chairs. Notice that these chairs are covered with small holes. Approximately how many holes are there on one chair (hint: you do not need to physically count all the holes)? On all of the chairs?
Classroom Building

In the West hallway of the Classroom Building there is a cabinet containing several computer diskettes. Using the information given to you about the storage capacity of each of the diskettes in the cabinet create a graph. What observations can be made by looking at the graph youíve created? Is there a visible trend in the advancement of technology?
Walk up the stairs toward the third floor. On the way stop at one flight of stairs and answer the following Question: Calculate the most comfortable height of a step to climb. To do this, each student will lift their leg up to a comfortable height and measure the distance from the sole of their shoe to the floor. Find the average of the comfortable step height. What is the height of the step in the staircase?
On the third floor find the Map Library (Rm. 317). On the wall there is a topographic map. This question deals with a simple way to calculate and use Scale on maps. How could you express the 2cm to 100,000cm as a representative fraction or ratio? Using your previous answer, calculate how many metres you would travel in real life if you traveled 5cm on your map? Explain your answers. (Remember that 1cm = 0.01m)
Library Building

As you stand in the foyer of the main library, what architectural forms are noticeable? How could a mathematician represent these forms?
Phil does not mind photocopying reference material and he is rather speedy at it. If he can do so at the rate of 4 sheets a minute, how much would Phil have to charge other students per page to do their photocopying for them if he did not wish to make any less than 6.50$ an hour. It costs Phil 7¢ a page to photocopy.
How many tables are there on the 3rd floor? Assuming 2 people can sit comfortable on one side of a table, how should the tables be arranged to accommodate a maximum number of students? A minimum? At present, how many students can occupy tables on the 3rd floor?
Ad Hum Building

Make the Pit wheel chair accessible. How long of a board and at what angle would it be for that length to be appropriate?
Go to the elevators. Weigh yourself before you get in; weight yourself when the elevator is going up and down. What did you notice? Why?
Why were the stairs not put in visible view from the pit? (stairs on the 2nd and 3rd floors)
Extra: for anywhere there are bike racks
Why are the bike racks shaped the way they are? Is this shape the strongest? Can you think of a structure that might work better? If so, why?
Language Institute

- The residential area at the Language Institute has a very interesting shape- it is in the form of a rectangle with a pyramid structure on top. Students can stand outside the L.I. building and draw a sketch of the interestingly shaped residential area of the L.I. They will be asked to come up with a formula representing their sketch along with an approximate value for the volume of their sketch.
The Language Institute has a cafeteria on the second floor called The Café Des Lys. This cafeteria caters to the general public and to the L.I. residents. Residents are given meal cards which are filled at 60 dollars at a time and which provide an overall $900 eating allowance for the entire spring semester. Students should be given a copy of the menu board, and from it, devise a budget scheme which would enable a resident to have a nourishing breakfast, lunch and supper every day over the course of the semester within the $900 budget that they are given.
There are two major hallways on the first floor of the Language Institute. One is in the shape of a straight line, the second is in the shape of a semicircle or parabola. Try to get the students to discover this observation and represent the hallways as 1) the equation of a line and 2) as a parabolic equation.
Campion

*A 30cm ruler will be needed for the majority of the questions.
Go to the silver spiral located at the main entrance of Campion College. To the west of the spiral is a collage with a picture of the floor display. Assume that this picture is 1/8th the size of the real floor display. Use information from the picture to determine the area of the circle in the real floor display.
Enter Campion and go down the ramp into the pit area. If you look at this ramp from the side you will notice that it is a right-angle triangle. Find the angle of elevation of the ramp from pit floor to the next level. In order to find this angle you will first need to know the height and length of the base of the ramp or triangle. The height can be attained using the stairs located on the other side of the pit while the length of the base can be found using the individual strips of wood on the floor. Hint: use the larger squares of wood when possible to speed up the process. Once the angle of elevation has been found, find the length of the remaining side or hypotenuse.
After such an exhausting previous question you decide to go Roca Jackís, located in Campion, and order some food. You decide you would like a large coffee and a bagel. How much will this entire purchase cost with a 7% tax? Now go to the Luther concession stand and attempt to order the same combination. How much would this purchase cost with a 7% tax? Which college offers the better deal?
Luther 
Go to the second floor of Luther College and find room 208. Between the doors of room 208 you will notice five pictures. Consider each of these pictures as an individual set, call them sets A, B, C, D and E (going left to right).
- Which sets have more people wearing glasses in them, A or B , C or D?
- How many females are there in sets C or E?
- Using only sets A and B draw a Venn diagram representing three criteria. The criteria
to be represented are people with long hair, people wearing a bow tie and people wearing glasses. After you have
completed the diagram report how many people contain all three criteria.
Go to the Chapel on the second floor of Luther (just down the hall from room 208). Beside the Chapel there is a flight of stairs that lead all the way to the basement level of Luther. Using only one ruler measurement, figure out the distance from the basement level to the floor of the second level (the floor you are standing on).
Physical Activity Centre (PAC) 
Go up to the Fitness and Lifestyle Centre. Head over to the bench press area. How many different combinations can you make with the different weights (45, 35, 25, 10, 5 lbs weights) for 225 lbs? You can only on put 5 weights per side. You must have even weights on both sides. Note: the bar is 45 lbs.
Go to the gym. Start on the baseline of the basketball court. Walk to the other baseline and count the number of steps it takes you get there. Do the same thing for jogging and for sprinting. Calculate the number of steps it would take you to travel 1 mile for all three method s of transportation. (a basketball court is 84 feet long and there are 5,280 feet in a mile)
Education Building

- How many different ways/routes are there to get to the computer lab on the second
floor from the main floor?
Draw a floor plan with the routes on it.
Education Cafeteria
Using the utensil and condiment compartments. How many different ways can you put /arrange the trays in the compartments?
-
Look at the lights from different angles. What happens to the shape of the fixture, brightness of light, shadows?
Why did the engineers build this building the way they did? (maximum, minimum area)
Ex: Some shelves are built into the walls to maximize space.
Look at the hallways, stairways, lockers, ed pit, etc.